MÉCANIQUE CÉLESTE

MÉCANIQUE CÉLESTE

Le but de la mécanique céleste est de prévoir, avec le plus d’exactitude possible et pour des époques aussi éloignées que possible dans le passé ou dans l’avenir, la position dans l’espace des corps célestes: planètes, satellites, étoiles...

La mécanique céleste classique a pour principal objet le mouvement des corps du système solaire. Elle s’appuie sur les principes suivants, établis par Galilée et Newton au XVII^e siècle:

– L’espace est euclidien à trois dimensions, et le temps est un paramètre variant de moins l’infini à plus l’infini, indépendant du système de référence spatial envisagé.

– Il existe une infinité de repères fondamentaux, appelés repères inertiels, qui sont tous animés d’un mouvement de translation rectiligne et uniforme les uns par rapport aux autres et qui sont tels que tout point matériel qui n’est soumis à aucune force est soit au repos dans l’un de ces repères, soit animé d’un mouvement rectiligne et uniforme.

– Dans un repère inertiel, un point soumis à une force représentée par le vecteur づ prend une accélération représentée par le vecteur ゔ, liée à づ par la relation:

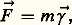la constante de proportionnalité m étant appelée la masse inerte du point ou, tout simplement, sa masse. On appelle point matériel un point géométrique affecté d’une masse. On sera donc amené à supposer que l’on est capable de recenser à coup sûr toutes les actions physiques agissant sur un point matériel et à les représenter sous la forme d’un vecteur づ, fonction de la position du point, de sa vitesse et d’autres paramètres, de telle sorte que l’accélération soit donnée par la formule ci-dessus. Si elle ne l’est pas, c’est que le référentiel considéré n’est pas galiléen, et on doit alors introduire des forces fictives appelées force d’inertie d’entraînement et force complémentaire de Coriolis.

– Si un point matériel A exerce sur un point matériel B une force représentée par le vecteur づ, le point B exerce sur le point A une force représentée par le vecteur 漣 づ (principe de l’action et de la réaction).

– La loi de la gravitation universelle de Newton s’énonce ainsi: un point matériel est soumis de la part d’un autre point matériel à une force attractive représentée par un vecteur porté par la droite qui joint les deux points et dont la grandeur est inversement proportionnelle au carré de leur distance.

La constante de proportionnalité est le produit d’une constante universelle, G , appelée constante de la gravitation par deux grandeurs appelées les masses graves de chacun des points. Le principe d’équivalence énonce que masses inertes et masses graves sont égales; on les désigne simplement par le nom de masses . Dans le système SI, G a pour valeur 6,672 59 憐 10 size=1^漣11 m³.kg size=1^漣1.s size=1^漣2.

Nous verrons comment on établit les équations différentielles du mouvement de n points matériels. Leur intégration, très difficile, conduit à des solutions, presque toujours approchées, qui dépendent d’un certain nombre de constantes d’intégration qui, en astronomie, sont fournies par les observations.

Dans certains cas, les corps dont on étudie le mouvement ne peuvent être réduits à des points matériels; il faut faire appel à des systèmes matériels qui, pour la mécanique céleste du système solaire, sont souvent assimilés à des corps solides.

Il arrive que la résolution concrète d’un problème de mécanique céleste conduise à tenir compte de forces annexes qui ne sont pas d’origine gravitationnelle (frottement atmosphérique sur un satellite artificiel proche de la Terre), ou qui ne dérivent pas d’une fonction de force (forces dissipatrices dues aux marées). On en tient compte dans la mesure où l’on sait donner à ces forces une expression mathématique rigoureuse.

La théorie de la relativité générale donne de la gravitation une interprétation géométrique: l’espace-temps est courbé par la présence de matière, et d’euclidien devient riemannien. Les trajectoires des corps célestes, associées à la loi du temps sur ces trajectoires, sont alors interprétées comme étant des géodésiques de l’espace-temps. S’il résulte de cette conception une modification profonde des équations de la mécanique céleste, il n’en reste pas moins que les méthodes classiques de la mécanique newtonienne, plus simples à utiliser, donnent très souvent une approximation suffisante pour les besoins des astronomes, dans la mesure où ces derniers considèrent des champs faibles et des vitesses petites par rapport à celle de la lumière. Cependant, les observations ont atteint un tel degré de précision qu’on ne peut plus négliger les effets relativistes, qui sont introduits sous forme de corrections dans les théories traditionnelles.

1. Le mouvement des deux corps

Cas général

Le point B étant soumis à une force centrale constamment dirigée vers A, le mouvement se fait dans un plan passant par A et par le vecteur vitesse initiale ふ⁰ ayant pour origine la position initiale B⁰ (fig. 1). Ce mouvement se fait suivant la loi des aires , c’est-à-dire que le rayon AB balaie au cours du mouvement des aires égales en des temps égaux.

Prenons, dans le plan de cette orbite plane, un système de coordonnées polaires d’origine A et d’axe polaire AB⁰; r est le rayon vecteur, l’angle polaire. La loi des aires donne:

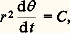C étant une constante.

Le théorème des forces vives donne:

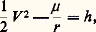où V est le module du vecteur ふ, 猪 le produit de la constante de la gravitation universelle par la somme des masses de A et de B, et h une constante. Mais on a aussi:

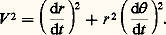Cette équation et les deux précédentes donnent, en éliminant le temps, l’équation différentielle de la trajectoire:

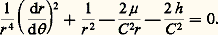On peut facilement intégrer cette équation en posant:

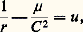et l’on trouve:

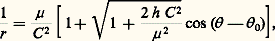⁰ étant une constante. L’équation trouvée est l’équation d’une conique de foyer A (première loi de Kepler) et de paramètre C ²/ 猪 . L’axe focal est l’axe = ⁰, et l’excentricité est le radical qui est en facteur de cos( 漣 ⁰). Par conséquent, le genre de la conique ne dépend que du signe de h . Or, d’après le théorème des forces vives:

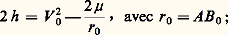donc, si V ⁰ est plus petit que 連2 猪 /r ⁰, la trajectoire est une ellipse; s’il est plus grand, la trajectoire est une hyperbole. Si V ⁰ est égal à 連2 猪 /r ⁰, la trajectoire est une parabole; on désigne parfois cette quantité par l’expression vitesse parabolique .

La trajectoire sera un cercle si ふ⁰ est perpendiculaire à AB⁰ et si l’excentricité est nulle. On montre facilement qu’il faut que V ⁰ = 連 猪 /r ⁰ pour qu’il en soit ainsi.

Le mouvement képlérien

Quand la trajectoire de B est une ellipse, le mouvement est dit képlérien. Ce mouvement joue un rôle particulièrement important en mécanique céleste.

Soit O le centre de l’ellipse décrite par B; on rapporte l’ellipse à un système d’axes rectangulaires d’origine O, l’axe Ox étant porté par OA et orienté de O vers A. Le sommet du grand axe de l’ellipse le plus voisin du foyer A, soit P sur la figure 2, s’appelle le périastre (périhélie si A est le Soleil, périgée si A est la Terre). L’autre sommet P est l’apoastre (aphélie ou apogée ). L’angle v = P brigitteuang;AB est l’anomalie vraie du point B; si B est le point du cercle principal de l’ellipse dont B est la projection, l’angle E = x brigitteuang;OB est l’anomalie excentrique de B. On désigne par a le demi-grand axe de l’ellipse. Le paramètre est p = a (1 漣 e ²); il est aussi égal à C ²/ 猪 ; donc, C ² = 猪 a (1 漣 e ²). Comme l’aire totale de l’ellipse est 神a ² 連1 漣 e ², on a aussi, en appelant T la période du mouvement (le temps que met B pour faire un tour complet de l’ellipse):

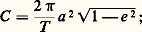donc:

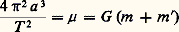ou: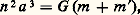

en posant n = 2 神/T . La relation trouvée prend le nom de troisième loi de Kepler . C’est Kepler en effet qui a trouvé empiriquement à partir des observations l’expression cidessus dans laquelle cependant il négligeait m , masse d’une planète, très petite devant m , masse du Soleil. Il en résultait que, pour lui, les cubes des demi-grands axes de toutes les planètes étaient proportionnels aux carrés de leurs périodes de révolution.

L’aire du secteur elliptique HPB est la projection de l’aire du secteur circulaire HPB du cercle principal de l’ellipse sur le plan de celle-ci; l’aire HPB est donc égale à l’aire HPB multipliée par 連1 漣 e ².

Or l’aire HPB est égale à la différence entre l’aire a ² E /2 du secteur OPB et l’aire du triangle OHB , égale à (a ²e sin E )/2. On aura donc, si t 漣 精 est le temps mis par le point B pour aller de P en B :

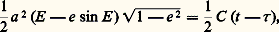d’où l’équation de Kepler :

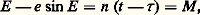qui permet de calculer la position de B sur son orbite pour un instant donné. L’angle M , proportionnel au temps, s’appelle l’anomalie moyenne .

L’orbite képlérienne est définie dans son plan si l’on connaît le demi-grand axe a , l’excentricité e et l’un des temps de passage au périastre 精 . Il reste à placer l’orbite dans l’espace. Pour cela, on considère en général un système d’axes de coordonnées rectangulaires d’origine A, soit Ax, Ay, Az (fig. 3). L’orbite coupe le plan Ax, Ay en deux points alignés avec A qu’on appelle les nœuds . Le nœud N où passe le point B quand il va du côté des z négatifs vers les z positifs est le nœud ascendant . L’orbite est complètement définie dans l’espace quand on connaît l’angle 行 entre Ax et AN, l’inclinaison i du plan de l’orbite sur le plan Ax, Ay et l’angle 諸 entre AN et la direction du périastre AP.

2. Le problème des n corps

Équations du mouvement des n corps

Soient O l’origine d’un système de référence absolu et n corps Pⁱ de masses m ⁱ . Les équations du mouvement du corps Pⁱ sont:

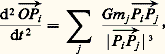où j varie de 1 à n sans prendre la valeur i . Il y aura donc 3n équations différentielles du second ordre à intégrer pour connaître le mouvement des n corps. Seules dix intégrales premières du mouvement sont connues, et Henri Poincaré a montré qu’il n’existait pas d’autres intégrales premières uniformes du mouvement. On trouve ces intégrales premières de la façon suivante.

Tout d’abord, soit I le centre des masses des n corps défini par:

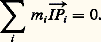On en tire:

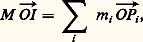où M est la somme des masses m i . En dérivant deux fois et compte tenu des équations générales écrites plus haut, on déduit que:

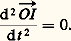Le point I a donc un mouvement rectiligne et uniforme, ce qui donne six intégrales premières correspondant aux six constantes d’intégration du mouvement du centre des masses. Par ailleurs, puisqu’il n’y a pas de forces extérieures au système des n points, le moment cinétique en O du système est constant :

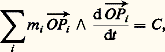où ぢ est un vecteur constant, ce qui donne trois intégrales premières correspondant aux trois composantes de ce vecteur.

Enfin, le théorème des forces vives fournit la dixième intégrale première:

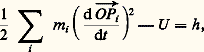où h est une constante et où U est le potentiel défini par:

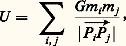i étant différent de j .

Ces intégrales premières sont en nombre insuffisant pour qu’on puisse intégrer les équations du mouvement, sauf si n = 2. C’est le mouvement des deux corps, qui est étudié dans le paragraphe précédent. On indiquera plus loin les différentes méthodes qui permettent de résoudre le problème des n corps.

Le problème d’un grand nombre de corps quelconques

Si l’on considère le problème des n corps dans toute sa généralité, on doit résoudre les équations du mouvement pour n corps de masses comparables entre elles, n étant aussi grand que l’on veut, les positions et les vitesses initiales étant distribuées de façon quelconque. C’est le cas, par exemple, dans les ensembles d’étoiles, amas galactiques, amas globulaires, galaxies. Il n’est pas question d’intégrer séparément les équations du mouvement de chacune des étoiles, mais, en revanche, on souhaite connaître l’évolution globale, dans le passé et dans l’avenir, de l’ensemble. On cherche, par exemple, à savoir si un amas va se disperser complètement dans l’espace et en combien de temps, ou bien si, au contraire, les étoiles qui le forment resteront toujours groupées. Pour cela, on fait appel à certaines hypothèses simplificatrices, par exemple que les étoiles ont une distribution sphérique, leur densité numérique augmentant vers le centre. On caractérise l’ensemble des n corps non pas par les coordonnées de chacun d’eux, mais par un nombre limité de paramètres auxquels on applique des théorèmes connus de la mécanique, comme le théorème du viriel. On peut aussi suivre l’évolution des paramètres choisis au moyen d’intégrations numériques rendues faciles et rapides par l’utilisation d’ordinateurs. Cette branche de la mécanique céleste porte le nom de dynamique stellaire .

Les équations aux perturbations

Dans le système solaire, la distribution des masses, des positions et des vitesses est particulière et permet de résoudre le problème des n corps par des méthodes d’approximation.

La masse du Soleil est beaucoup plus grande que celles des planètes, puisque la plus massive d’entre elles, Jupiter, a une masse mille fois plus faible. Il en résulte que la seule force notable qui agit sur une planète est la force d’attraction du Soleil. On est ramené au mouvement de deux corps, le Soleil et la planète, qui a donc un mouvement képlérien autour du Soleil. L’attraction des autres planètes crée des petites perturbations de ce mouvement képlérien. S’il s’agit du mouvement de la Lune autour de la Terre, ou du mouvement d’un satellite autour d’une planète, là encore un mouvement képlérien du satellite autour de sa planète constitue une bonne approximation, car le corps perturbateur principal, qui est ici le Soleil à cause de sa grande masse, est à une distance très grande par rapport à la distance du satellite à sa planète.

De même, un satellite artificiel proche de la Terre a, en première approximation, un mouvement képlérien autour du centre de celle-ci, car la Terre est en première approximation une sphère homogène. Il faudra ensuite tenir compte des perturbations apportées par le fait que la Terre est aplatie.

Dans tous ces cas, les équations du mouvement d’un astre M de coordonnées rectangulaires x , y , z peuvent alors être mises sous la forme:

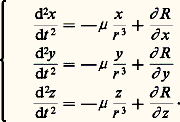猪 est une constante et R une fonction des coordonnées x , y , z , des coordonnées des corps perturbateurs ou de constantes caractérisant le corps central (aplatissement) et éventuellement du temps. Cette fonction R est petite car, ou bien elle a en facteur un petit paramètre – masse du corps perturbateur, exprimée en masse solaire, ou aplatissement dynamique du corps central –, ou bien elle contient au dénominateur la distance, supposée grande, du corps perturbateur (cas de la Lune et des satellites des planètes). La fonction R porte le nom de fonction perturbatrice .

Si l’on suppose que R s’annule à un instant donné, les équations précédentes sont celles du problème des deux corps, que l’on sait intégrer. L’orbite est une ellipse appelée orbite osculatrice et qui est caractérisée par les six constantes définies plus haut (a , e , i , 行 , 諸 , 精 ), appelées éléments osculateurs . On utilise ensuite la méthode de la variation des constantes, introduite par Lagrange, qui conduit aux équations ci-dessous, dites équations de Lagrange :

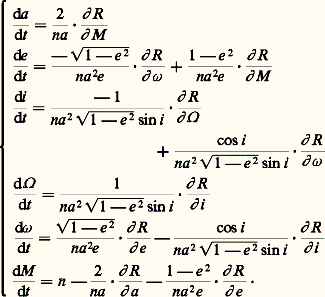Dans les équations en a , e , i ne figurent que les dérivées partielles de R par rapport à 行 , 諸 et M , et inversement. Les variables a , e , i sont appelées variables métriques, et les variables 行 , 諸 , M , variables angulaires. Bien entendu, si R est négligeable, tous les seconds membres sont nuls et, par conséquent, a , e , i ... sont constants, à l’exception de M , car, si R est nul, on a:

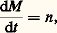et, en intégrant:

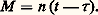Au lieu des variables a , e , i ..., dites variables elliptiques, on utilise parfois les variables de Delaunay, L, G, H, l, g, h :

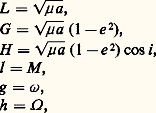qui vérifient le système canonique suivant:

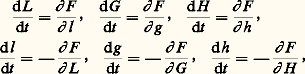où le hamiltonien F a pour expression:

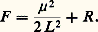On utilise aussi, surtout pour les théories planétaires, d’autres variables, les variables canoniques dites de Poincaré, qui sont bien adaptées au cas où les excentricités et les inclinaisons sont faibles.

Pour résoudre les équations de Lagrange ou de Delaunay, on procède généralement par approximations successives. On néglige tout d’abord R , les seconds membres sont nuls, sauf celui de l’équation en M (ou l ), qui est constant. Les variables sont constantes, sauf M (ou l ), qui est une fonction linéaire du temps. On reporte alors cette solution dans les seconds membres complets qu’on aura développés en séries trigonométriques de M (ou l ) et des angles analogues se rapportant aux corps perturbateurs. On intègre terme à terme, et on obtient ainsi une solution au premier ordre du petit paramètre. Chaque variable est maintenant égale à une constante augmentée de termes dépendant du temps qui sont soit périodiques, soit séculaires, c’est-à-dire sous forme de polynômes du temps. On substitue de nouveau cette solution dans les seconds membres pour avoir la solution au deuxième ordre du petit paramètre et ainsi de suite.

Si l’on utilise un système canonique, comme celui de Delaunay, on lui applique des méthodes classiques de résolution de tels systèmes.

Perturbations ne dépendant pas d’un potentiel

Il arrive que les perturbations causées au mouvement képlérien d’un astre proviennent de forces qui ne dérivent pas d’un potentiel. C’est le cas, par exemple, du mouvement d’un satellite artificiel de la Terre soumis au frottement atmosphérique quand son orbite est assez basse. On remplace alors les équations de Lagrange par des équations analogues où figurent, dans les seconds membres, non pas la fonction R , mais les composantes de la force perturbatrice sur trois axes convenablement choisis qui sont en général la tangente à la trajectoire osculatrice au point considéré, la normale et la perpendiculaire au plan de la trajectoire.

3. Mécanique céleste du système solaire

Les théories planétaires

Soit x ⁱ , y ⁱ , z ⁱ les coordonnées rectangulaires d’une planète Pⁱ de masse mⁱ dans un système d’axes ayant pour centre le Soleil O, de masse prise pour unité. Soient rⁱ la distance OPⁱ et r^ij la distance Pⁱ P^j de la planète Pⁱ à une autre planète P^j de masse m^j . Des équations du problème des n corps données ci-dessus, on déduit facilement:

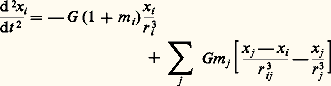et deux équations analogues en yⁱ et zⁱ . Dans l’équation ci-dessus, j prend toutes les valeurs de 1 à n (n étant le nombre des planètes envisagées), à l’exception de la valeur i .

Posons:

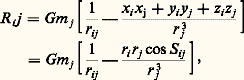où S ij est l’angle des directions OPⁱ et OP^j . R^ij est la fonction perturbatrice de la planète Pⁱ due à la planète P^j . La fonction perturbatrice totale de Pⁱ est:

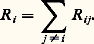On développera la fonction perturbatrice en développant chaque fonction R^ij sous la forme suivante:

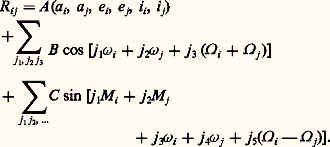Les coefficient B et C dépendent, comme A , des éléments métriques; les sigma signifient qu’il faut tenir compte d’un grand nombre de termes correspondant à des systèmes de valeurs différents des entiers positifs, négatifs ou nuls j ¹, j ², j ³, ..., les coefficients B et C changeant avec chaque combinaison.

Pour intégrer, on peut procéder par approximations successives selon le schéma indiqué plus haut. On voit que, lorsqu’on substitue la solution d’ordre zéro, correspondant à des mouvements képlériens pour toutes les planètes, dans les seconds membres et qu’on intègre, il apparaît des termes séculaires provenant des termes de la fonction perturbatrice qui ne contiennent pas les fonctions linéaires du temps Mⁱ et M^j . Aux ordres plus élevés que le premier, on voit apparaître des termes contenant des puissances du temps plus grandes que un et même des termes de Poisson , produits de fonctions périodiques par des puissances du temps. Ces termes semblent indiquer que le système solaire est instable, puisque certains éléments des orbites croissent au-delà de toute limite. Cela est dû en grande partie à la façon dont on est amené à conduire les calculs au cours des diverses itérations; Laplace a montré que, jusqu’à un certain ordre des masses, le système solaire est stable, résultat dont doutait Leverrier et qui sera en partie contredit par Poincaré.

Le mouvement de la Lune

Le corps central est ici la Terre de masse M ; m est la masse de la Lune et m celle du Soleil.

Les équations s’écrivent toujours sous la forme:

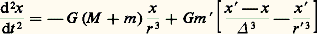et de façon analogue en y et z . Ici, x , y , z sont les coordonnées de la Lune, x , y , z celles du Soleil; est la distance Lune-Soleil.

La fonction perturbatrice est alors:

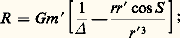elle reste peu importante en comparaison du terme principal des équations. En effet, si m est très grand, en revanche et r sont environ 400 fois plus grands que r . Les petits paramètres par rapport auxquels on développe la solution du problème sont le rapport des demi-grands axes des orbites de la Lune autour de la Terre et de la Terre autour du Soleil (ou le rapport du moyen mouvement du Soleil à celui de la Lune, qui lui est lié directement), ainsi que l’excentricité et l’inclinaison de l’orbite de la Lune.

L’intégration met en évidence des inégalités du mouvement de la Lune dont certaines sont connues par l’observation depuis très longtemps, comme l’évection, qui est une inégalité d’environ 1⁰14 dans la longitude. On calcule, à l’heure actuelle, des milliers de tels termes dans la position de la Lune.

Les théories du mouvement de la Lune les plus remarquables sont celle de Charles Delaunay, au XIX^e siècle, et d’Ernest William Brown, améliorée par Wallace Eckert dans la première moitié du XX^e siècle. On utilise en France, depuis 1984, l’éphéméride lunaire parisienne calculée au Bureau des longitudes.

Le mouvement des satellites artificiels

Le potentiel gravitationnel créé par un corps solide, par exemple la Terre, en un point extérieur à ce corps peut se développer en fonctions harmoniques sphériques sous la forme suivante:

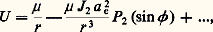où 﨏 est la latitude du satellite au-dessus du plan équatorial, r sa distance au centre de la Terre, P ² (sin 﨏) le polynôme de Legendre en sin 﨏 d’orde deux, a ^e le rayon équatorial de la Terre (6 378 140 m) et J ² un coefficient sans dimension qui, pour la Terre, est égal à 1/1 000 environ. Le développement contient de nombreux autres termes que l’on n’a pas écrits ici. Certains, les harmoniques zonaux , ne dépendent, comme le terme en J ² ci-dessus, que de r et de 﨏; d’autres, les harmoniques tesséraux , dépendent aussi de l’ascension droite du satellite, donc de la longitude du satellite et du temps sidéral. Les coefficients Jⁿ et J n k de tous les harmoniques sont petits, au maximum de l’ordre du carré du plus grand d’entre eux, J ² (J ¹ est nul si, comme on le fait toujours, on prend l’origine des coordonnées au centre de la Terre). On procède en utilisant la méthode des perturbations, la fonction pertubatrice étant:

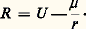L’orbite peut être considérée, en première approximation, comme une ellipse ayant pour foyer le centre de la Terre, qui tourne dans son plan et dont le plan tourne autour de l’axe de rotation de la Terre.

Mouvement d’un astre autour de son centre de gravité

Cette étude est particulièrement intéressante pour la Terre, dont la rotation est à l’origine de la définition de l’échelle de temps dite temps universel .

La Terre étant considérée comme un corps solide, soit A , B , C ses moments d’inertie par rapport à trois axes rectangulaires ayant pour origine le centre de la Terre et liés à celle-ci. Soient p , q , r les composantes dans ce système d’axes du vecteur vitesse instantanée de rotation.

Ces quantités sont liées par les équations différentielles d’Euler:

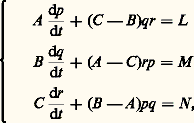où L , M , N sont les composantes du couple exercé sur l’ellipsoïde terrestre par le Soleil et par la Lune; ce sont des fonctions des coordonnées de ces astres que l’on développe en séries trigonométriques. On trouve ainsi qu’en première approximation la Terre a une rotation uniforme autour d’un axe dont la direction décrit en 26 000 ans un cône de 23⁰30 de demi-angle au sommet (phénomène de précession ). L’axe de rotation a de plus un mouvement de balancement de faible amplitude et de période voisine de 18 ans autour de sa position moyenne (phénomène de nutation ).

En fait, le phénomène est complexe, d’autant plus que la Terre n’est pas un solide indéformable. Les théories et les observations relatives à la rotation terrestre sont centralisées par l’International Earth Rotation Service (cf. TERRE - 2 Mouvements de la Terre ).

Intégration numérique

Quelle que soit la complexité des équations de la mécanique céleste, on a toujours la ressource de les intégrer numériquement. Pour cela, on part de valeurs connues des positions et des vitesses du corps considéré pour un instant donné, et on calcule les valeurs numériques des forces qui agisse sur lui à cet instant. Cela permet d’extrapoler les valeurs des positions et des vitesses pour un instant séparé de l’instant initial d’un pas qu’on se donne à l’avance. On recommence ensuite le processus autant de fois qu’on veut, sans oublier que la solution se dégrade quand on s’éloigne de l’instant initial, et ce d’autant plus que les conditions initiales sont mal connues et que les erreurs d’arrondis dans les calculs sont importantes. Les puissants ordinateurs dont on dispose aujourd’hui permettent de réaliser des intégrations numériques où l’on tient compte d’un grand nombre de forces et d’un grand nombre d’observations. C’est ainsi que le Jet Propulsion Laboratory, aux États-Unis, a calculé des éphémérides très précises des corps du système solaire, largement utilisées et qui sont connues sous les noms de DE 200, DE 102 ou DE 118.

Cependant, les théories analytiques sous forme littérale ou semi-analytique, comme les théories VSOP et TOP, pour les planètes, ou ELP (éphéméride lunaire parisienne), pour la Lune, qui sont développées en France, au Bureau des longitudes, restent fondamentales. Elles permettent d’apprécier la contribution de chacune des forces envisagées, dont les effets ne sont pas mêlés, comme dans l’intégration numérique, et de modifier facilement l’éphéméride quand des valeurs nouvelles de certaines constantes, comme les masses, viennent à être connues.

4. Problèmes généraux classiques et modernes

Orbites périodiques. Résonance

Des résultats théoriques importants concernant le problème des trois corps ont été obtenus en introduisant des orbites particulières, appelées orbites périodiques. Les premières ont été trouvées par Lagrange, et la théorie complète en a été faite par Poincaré.

Considérons un système d’équations différentielles de la forme:

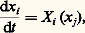où i et j varient de 1 à n , et tel que les fonctions Xⁱ soient des fonctions des p premières variables xⁱ de période 2 神. Supposons qu’une solution du système xⁱ = 﨏ⁱ (t ) ait la propriété suivante: quant t augmente de T , les p premières variables augmentent de 2 神, les autres restant inchangées. Une telle solution est dite périodique. Poincaré a cherché des solutions périodiques des équations de la mécanique céleste. Les conditions initiales dans le système solaire ont des probabilités nulles pour que les orbites correspondantes soient périodiques, mais les orbites véritables peuvent en différer très peu. Comme l’a dit Poincaré, il s’agit de «la seule brèche par où nous puissions essayer de pénétrer dans une place jusqu’ici réputée inabordable».

Les solutions périodiques sont classées en trois catégories. La première correspond à des mouvements plans et quasi circulaires, la deuxième à des mouvements plans mais où les orbites ont une excentricité non négligeable, la troisième à des inclinaisons non nulles.

Un des problèmes de mécanique céleste théorique les plus classiques est le problème restreint des trois corps . Deux des corps, de masses 猪 et 1 漣 猪 , ont chacun un mouvement circulaire et uniforme autour de leur centre de gravité commun O; un troisième corps, de masse négligeable, est soumis à l’attraction des deux premiers et se déplace dans le plan de leurs orbites. On étudie le mouvement dans un système d’axes tournants d’origine O, l’un des axes passant constamment par les deux premiers corps. De nombreuses recherches ont été faites pour trouver des orbites périodiques du troisième corps dans le système d’axes tournants. Signalons à ce propos le cas particulier dit problème de Copenhague , pour lequel 猪 = 1/2.

Une orbite périodique célèbre est l’orbite variationnelle de Hill. On considère un système d’axes tournants ayant pour origine le centre de la Terre et dont l’un des axes de coordonnées est dirigé vers le Soleil, que l’on suppose à l’infini. Les axes tournent avec une vitesse angulaire constante égale à la vitesse angulaire moyenne de la Terre autour du Soleil. Le mouvement de la Lune, dont on néglige l’inclinaison de l’orbite, obéit alors à un système d’équations différentielles assez simple dont on peut trouver une solution périodique. Dans le système d’axes tournants, la Lune décrit une sorte d’ovale centré sur la Terre, l’orbite de Hill, qui a servi à Brown pour une théorie complète du mouvement de la Lune.

Citons aussi les orbites périodiques dont Lagrange avait démontré la possibilité: trois corps décrivent des orbites elliptiques semblables, ces trois corps restant constamment aux trois sommets d’un triangle équilatéral; il est curieux de signaler que cent ans après la découverte de Lagrange, on a effectivement trouvé des petites planètes, qualifiées de troyennes , qui occupent les sommets de deux triangles équilatéraux dont les deux autres sommets sont occupés par le Soleil et par Jupiter.

On a vu que, dans les équations de la mécanique céleste, apparaissent sous des fonctions sinus ou cosinus des combinaisons linéaires de fonctions linéaires du temps; par exemple, dans la théorie des planètes, ce sont les longitudes moyennes; dans la théorie du satellite artificiel, ce sont le temps sidéral et l’anomalie moyenne du satellite dans des termes provenant des harmoniques tesséraux. Si les coefficients du temps dans les différentes fonctions du temps qui interviennent sont commensurables, on pourra trouver des termes dont le coefficient du temps sous les fonctions sinus ou cosinus s’annule. Par intégration, ces termes donneront donc des termes séculaires. Il se peut qu’on rencontre des coefficients du temps non nuls mais très petits, qui correspondent donc à des inégalités de très longue période. En intégrant, on divise par ces coefficients du temps, qui engendrent donc des termes non seulement de longue période, mais aussi de grande amplitude. Le phénomène est un phénomène de résonance. Un terme de ce genre est créé par l’action mutuelle de Jupiter et Saturne. Les périodes de révolution de ces deux planètes sont dans un rapport voisin de 5/2, ce qui provoque une inégalité de période égale à 850 ans et dont l’amplitude, pour Saturne, est de l’ordre de 1⁰. La cause de cette grande inégalité de Jupiter et de Saturne a été trouvée par Laplace.

Les phénomènes de résonance compliquent beaucoup la mécanique céleste à cause des petits diviseurs qu’ils introduisent dans les équations.

Problèmes théoriques

D’un point de vue théorique, les mathématiciens s’attachent à trouver des séries qui représentent les mouvements d’une façon mathématiquement exacte. En effet, les astronomes utilisent comme solutions des équations de la mécanique céleste des séries de Fourier à plusieurs variables qui ne sont pas uniformément convergentes. Poincaré a attiré l’attention sur ce point et démontré pour quelles valeurs des petits paramètres les séries seraient convergentes; il a montré aussi qu’il était légitime de continuer à utiliser les séries classiques dans des intervalles de temps qui ne sont pas trop longs. Karl Fritiof Sundmann a trouvé des séries pour le problème des trois corps valables dans tous les cas, mais malheureusement très lentement convergentes.

Un célèbre théorème de Kolmogorov a aidé à préciser la structure de l’espace des phases d’un système dynamique à lagrangien. Dans le cas où le système a deux degrés de liberté, Vladimir I. Arnol’d et Jürgen K. Moser ont donné de ce théorème une formulation adaptée à la mécanique céleste (théorèmes appelés KAM) et montré que les séries peuvent être convergentes pour certaines conditions initiales, ce qui contredit en partie les résultats de Poincaré.

Depuis Tullio Levi-Civita (1873-1941) et George David Birkhoff (1884-1944), on a cherché, par des changements de variables appropriés, à éliminer les singularités du problème des n corps dues au fait que deux des corps peuvent entrer en collision. Ce fut l’objet, dans les années soixante, des travaux de Paul Kustaanheimo et Edward I. Stiefel.

Effets de marées

Depuis ces mêmes années soixante, on a étudié en détail les effets de marée dans le système solaire. On sait que les marées océaniques sont dues à la différence entre l’attraction gravitationnelle exercée par la Lune sur le centre de la Terre et sur les gouttes d’eau situées à sa surface. Le frottement de l’océan sur le fond des mers qui en résulte provoque un lent ralentissement de la rotation de la Terre. Le moment cinétique ainsi perdu est transféré au mouvement orbital de la Lune qui, de ce fait, s’éloigne de la Terre. Des effets de même nature ont provoqué dans le passé le ralentissement de la rotation de certains satellites de planètes qui, depuis lors, comme la Lune, présentent toujours la même face à leur planète.

Le chaos

Les résultats les plus récents et les plus inattendus dans le domaine de la mécanique céleste concernent le comportement chaotique du système solaire. Des intégrations numériques sur des périodes longues mais cependant inférieures à l’âge présumé de ce système montrent, tout au moins pour les planètes inférieures (Mercure, Vénus, la Terre et Mars), une sensibilité telle à de petites variations des conditions initiales que l’on peut dire que prévoir la position de ces astres au bout d’un temps assez long (quelques centaines de millions d’années) est impossible. Ces effets sont l’objet d’études approfondies.

● Mécanique céleste branche de l'astronomie qui a pour objet l'étude du mouvement des astres sous l'action de la gravitation universelle.

Encyclopédie Universelle. 2012.